Каждое новое значение an в такой последовательности является более точным приближением к исходному результату а.
Циклы, реализующие такую последовательность приближений/итераций, называются итерационными.
В итерационных циклах условие окончания цикла основывается на свойстве безграничного приближения значений an к искомому пределу с увеличением n. Итерационный цикл заканчивается, если для некоторого значения n выполняется условие:
, где ℇ - допустимая погрешность вычислений. При этом результат отождествляют со значением an , то есть считают, что an = a.
Пример
Вычслить значение функции y = cos(x) с погрешностью, используя разложение косинуса в ряд:
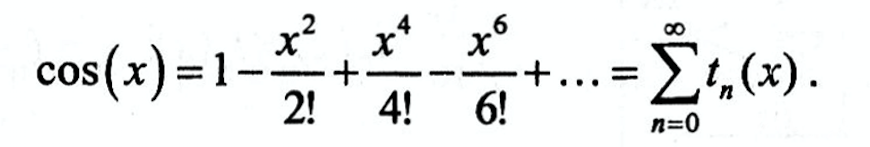
Накопление суммы производим по рекуррентной формуле:
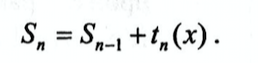
Здесь общий вид слагаемого суммы может быть записан в следующей форме:
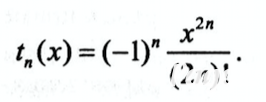
Для сокращения объема вычислений его целесообразно вычислять по формуле
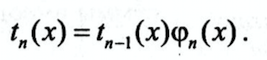
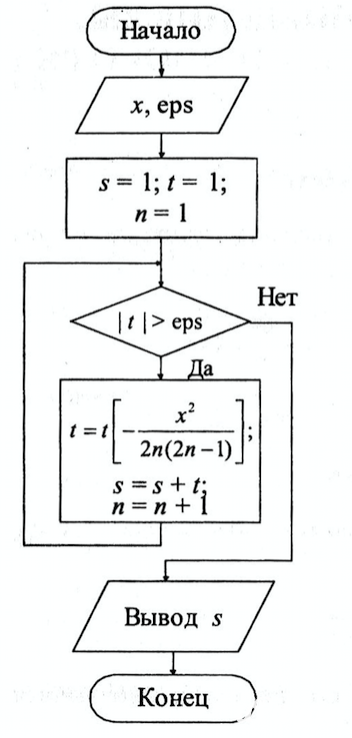
Блок-схема
Тогда текущий член ряда будет вычисляться по формуле:
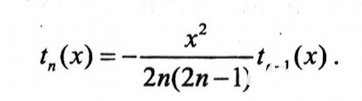
Начальное значение t0(x) находим подстановкой в формулу для общего члена tn(x) значения n=0
: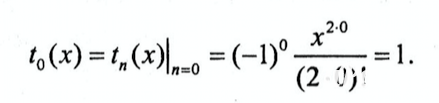
Начальное значение суммы можно принять равным первому члену ряда, то есть S0=1. Учитывая, что значения текущего члена ряда и суммы при n = 0 уже определены, номер члена ряда n примем равным единице.
На блок-схеме приведен алгоритм вычисления бесконечного ряда с заданной погрешностью eps.
Программа вычисления такой суммы имеет вид:
program laba8_v2;
Var {Описание переменных}
eps, s, t, x, u: real;
n: integer;
Begin
Write('Vvedite x = ');
Readln(x); {Ввод х}
Write('Vvedite eps = ');
Readln(eps); {Ввод погрешности}
Writeln('Dlya x = ', x:6:2, ' s pogreshnostiu = ', eps); {Вывод введеной информации}
u := 1; {Расчет нулевого слагаемого}
s := u; {Присваение сумме значения нулевого слагаемого}
n := 1; {Так как мы расчитали нулевое слагаемое, то выбрасываем иго из цикла}
while abs(u) > eps do {Как только слогаемое становиться меньше погрешности завершаем цикл}
begin
t := -x*x/(2*n*(2*n-1)); {Расчитываем фи}
u := u * t; {Умножаем фи на предыдущее слагаемое, таким образом получаем текущее слагаемое}
s := s + u; {Прибавляем текущее слагаемое к сумме}
n := n + 1; {Прибавляем к n единицу}
end;
Writeln('s = ', s:12:9, ' za ', n - 1, ' shagov'); {Выводим результат}
Writeln('Kontrolnoe znachenie: ', cos(x)); {Выводим контрольное значение для проверки}
Readln; {Задержка экрана}
End.
Статьи по программированию от спонсора данной статьи Eduget


